Sweetlemon 蒟蒻的拙作

（一）

开学了，高一(21)班共有$n (n\in \mathbb{N^{*}})$名同学，他们的学号分别是$1,2,\cdots,n$。班主任为了让同学们相互认识，想了一个好办法。

他在一次班会课上说：“同学们，如果你的学号是$x$，而另一个同学的学号是$y$，并且$x+y=2^{k}+2(k\in \mathbb{N})$，那么你们之间就有缘分。现在请你和所有与你有缘分的同学握手吧！”

(1) 当$n=30$时，求所有与$5$号同学握手的同学的学号。

(2) 求同学们握手的总次数。

(3) 班主任的办法很有效，握过手的两名同学互相成为了朋友。而且这种朋友关系还具有传递性，即如果甲、乙是朋友，乙、丙是朋友，那么甲、丙也是朋友。现在21班要组建一个团队参加比赛，为了保证团队的团结，要求团队中任意两人都是朋友。求团队中人数的最大值。

题解：

(1) $n=30$时，握手关系如下图：

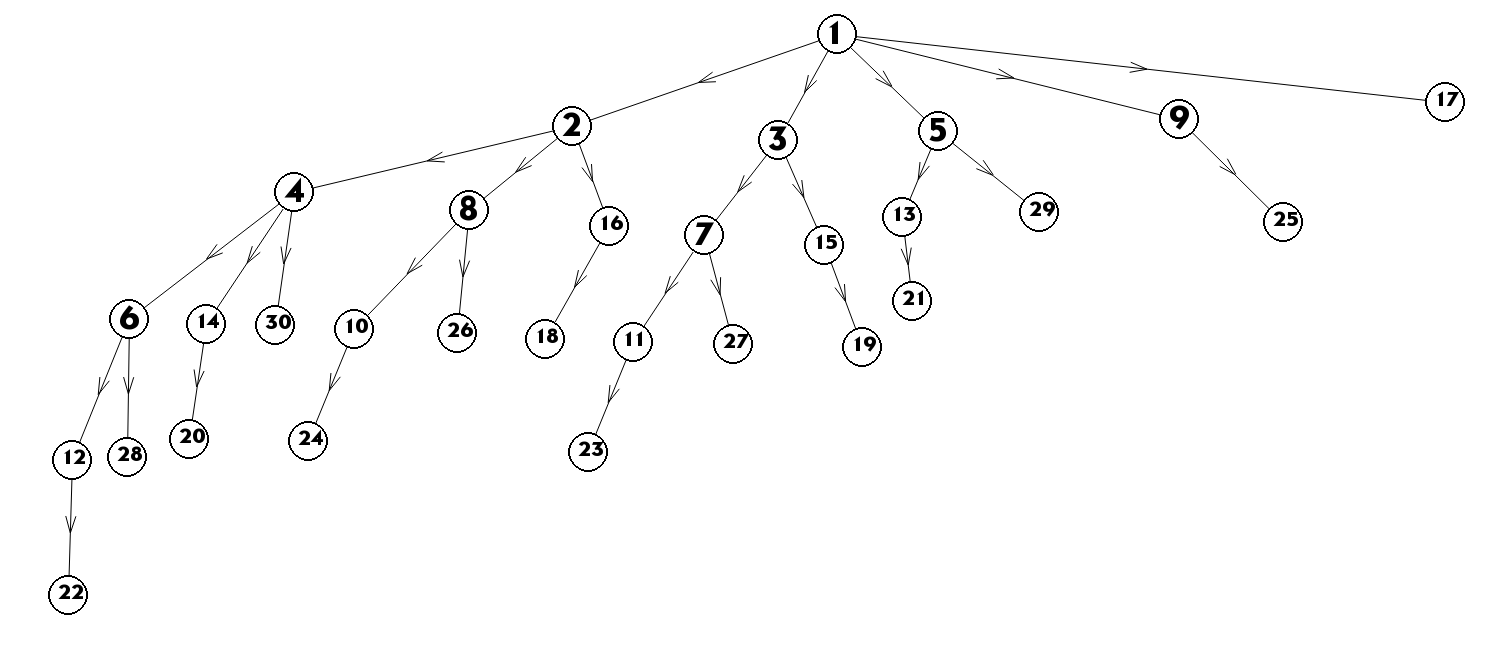
因此所有与$5$号同学握手的同学的学号所组成的集合为$\left \{ 1,13,29 \right\}$。

(2) 把$1$号同学称为“根”（可以理解为“全班的希望”）。

设$x$为集合$A=\left \{ x\in \mathbb{N} \mid 1<x\le n \right\}$中的任意元素。对于某一个$x$，设$y$是集合$\left \{ y\in \mathbb{N} \mid 1\le y< x \right\}$中的某个元素，且有$x+y=2^{k}+2(k\in \mathbb{N})$。如果存在这样的$y$，那么我们称$y$为$x$的“父亲”（$\sout{x}$被$\sout{y}$打败了，被迫承认的）。

下面我们证明，对于$A$中的每一个元素，都有且仅有$1$个父亲~~（废话，你还能认两个人作父亲？）~~。

整数$y$是$x$的父亲当且仅当$0<y<x$且$x+y=2^k+2$。

上述条件成立，当且仅当存在一个自然数$k$，使得$0<2^k+2-x<x$。调整得到$x<2^k+2<2x$，即$x-2<2^k<2x-2$。

下面证明对于每一个$x$，有且只有一个自然数$k$满足上式。

设$x-2=2^{a_1}+2^{a_2}+\cdots+2^{a_n}$
其中 $a_1>a_2>\cdots>a_n,\left\{a_1,a_2,\cdots,a_n\right\}\subseteq \mathbb{N}$。

则$x-2=2^{a_1}+2^{a_2}+\cdots+2^{a_n}\le 2^{a_1}+2^{a_1-1}+2^{a_1-2}+\cdots+2^{1}+2^{0}<2^{a_1+1}$

而$2x-4=2(x-2)=2^{a_1+1}+2^{a_2+1}+\cdots+2^{a_n+1}\ge 2^{a_1+1}$。

于是$x-2<2^{a_1+1}\le 2x-4$，知$x-2<2^{a_1+1}<2x-2$，知存在$k=a_1+1$使得上式成立。

再证明$a_1+1$是唯一满足条件的$k$。

若有$k'<a_1+1$满足上式，那么由$k'\in \mathbb{N}$知$k'\le a_1$，则$2^{k'}\le 2^{a_1}\le x-2$，与上式矛盾。

若有$k'>a_1+1$满足上式，那么由$k'\in \mathbb{N}$知$k'\ge a_1+2$，则$2^{k'}\ge 2^{a_1+2}>2^{a_1+1}+2^{a_1}+2^{a_1-1}+\cdots+2^1+2^0$。

而$2x-4=2^{a_1+1}+2^{a_2+1}+\cdots+2^{a_n+1}<2^{a_1+1}+2^{a_1}+2^{a_1-1}+\cdots+2^1+2^0$（此处请注意因为$a_1>a_2>\cdots>a_n\ge0$，所以$a_1+1>a_2+1>\cdots>a_n+1\ge1$。）

于是有$2^{k'}>2x-4$。

然而，若$x-2<2^{k'} <2x-2$，则有$2^{k'}<2x-2$，由$2^{k'}\in \mathbb{N}$知$2^{k'}=2x-3$，且由于$k'>a_1+1\ge1$知$2^{k'}$一定是偶数，出现矛盾。

综上，$a_1+1$是唯一满足条件的$k$。

由此，我们得出，对于$A$中的每一个元素，都有且仅有$1$个父亲。

考虑每一次握手，设握手的两人分别为$x$和$y$，不妨设$x>y$，则由上面的结论知$y$是$x$的父亲，因此每一次握手都仅在一个人和他的父亲之间发生~~（“发生”这个词好恐怖）~~，且学号大于$1$的每个人都会和他的父亲握手。

有多少对父子关系就有多少次握手。$1$没有父亲，而所有学号大于$1$的人都有父亲，因此同学们握手的总次数为$n-1$。

(3) 我们设$1$的祖先为$1$本身~~（我 生 我 自 己）~~，其余点的祖先定义为它父亲的祖先。（可以看上面的图帮助理解，按照图上的箭头反向往上走，走到最上面就是祖先。也可以理解为祖先是父亲的父亲的父亲的……父亲的父亲。）

用符号语言来表示，记一个人的父亲为$\text{par}(x)$，记一个人的祖先为$\text{gpar}(x)$。那么若$x=1$，则$\text{gpar}(x)=1$；否则$\text{gpar}(x)=\text{gpar}(\text{par}(x))$。如$\text{gpar}(2)=\text{gpar}(\text{par}(2))=\text{gpar}(1)=1$。

由父亲和祖先的定义知，一个人和他的祖先一定有朋友关系~~（怎么看着怪怪的）~~。

观察上面的图，我们发现图上每一个人的祖先都是$1$！这是不是巧合呢？

事实上，我们可以证明，任意满足$1\le x\le n$的整数的祖先都是$1$。

怎么证明呢？我们可以 感性理解 用数学归纳法。

首先，当$x=1$时，按照定义，欲证命题显然成立。

接着，我们设当$x\le k$时欲证命题成立，即“任意满足$1\le x\le k$的整数的祖先都是$1$”成立。下面我们要证明当$x=k+1$时命题也成立。

由(2)，$\text{par}(k+1)<k+1$，由于$\text{par}(k+1)\in \mathbb{N}$，知$\text{par}(k+1)\le k$，由归纳假设知$\text{gpar}(\text{par}(k+1))=1$。由祖先的定义知$\text{gpar}(k+1)=1$，即欲证命题在$x=k+1$时也成立。

根据数学归纳法，对任意满足$1\le x\le n$的整数，$\text{gpar}(x)=1$。

（由于我们还没有学过数学归纳法，因此这段证明过程在实际书写时可以略微 意会 调整。）

于是，每一个人都和$1$号同学是朋友。由朋友关系的传递性，全班同学都彼此是朋友。因此团队中人数的最大值为$n$。

这道题解完了，我们有什么收获呢？

我们要向高一(21)班的同学学习，让我们的班集体变得更团结~~，变得更团结的方式就是彼此认父亲，并发生握手关系~~。

（二）

有一个有限集$S=\left\{ a_1,a_2,a_3,\cdots, a_n\right\}$，并且设$A=\left \{x\mid x\subseteq S\right \}$。

现在已知映射$f_0:A\rightarrow \mathbb{R}$，设$A$上的映射$f_1,f_2,\cdots,f_n$，
对所有$1\le k\le n$的整数$k$，满足以下条件：

$\forall x\in A \ \ \wedge \ \ a_k\not \in x,\ \ f_{k}(x)=f_{k-1}(x)$

$\forall x\in A\ \ \wedge \ \ a_k\in x,\ \ f_k(x)=f_{k-1}(x)+f_{k-1}(\complement_{\left\{ a_{k} \right\} }x)$

请写出$f_{n}(S)$的值并给出证明。

（三）

有一个游戏，初始时$A=\left\{0\right\},B=\left\{-1\right\}$。游戏有$n$次操作，第$k(1\le k\le n)$次会从$A\cup B$中等概率随机选择一个数$x$，如果设这个数$x$所在的集合为$S(S\in \left\{A,B\right\})$，那么这次操作会将$S$变为$S\cup \left\{k\right\}$。求这$n$次操作后，$A$集合的元素数量是$t(1\le t\le n+1)$的概率。

题解

此概率与$t$无关，都为$\frac{1}{n+1}$。

有几种证明方法：

数学归纳法

设$g[i][j]$为进行了$i$次操作，$A$集合中有$j$个数的概率。

则$g[0][1]=1=\frac{1}{0+1}$，初始条件满足。

$\begin{aligned}g[i][j]&=\frac{j-1}{i-1+2}g[i-1][j-1]+\frac{(i-1+2)-j}{i-1+2}g[i-1][j]\\&=\frac{1}{i+1}((j-1)g[i-1][j-1]+(i+1-j)g[i-1][j])\end{aligned}$

此时若有$g[i-1][x]=\frac{1}{i}$（归纳假设），则

$\begin{aligned}g[i][j]&=\frac{1}{i+1}((j-1)g[i-1][j-1]+(i+1-j)g[i-1][j])\\&=\frac{1}{i+1}(j-1+i+1-j)\frac{1}{i}\\&=\frac{1}{i+1}\end{aligned}$

因此根据数学归纳法证毕。

臆想法

这一种方法需要很强的臆想能力。

把“选到的数在$A$中”记为$1$，“选到的数在$B$中”记为$0$。那么$n$次操作可以记为一个$01$序列，不妨记为$\left\{a_n\right\}$。记$\left\{a_n\right\}$的前$n$项和为$\left\{S_n\right\}$。令$S_0=0$。

我们首先计算“操作序列恰好是某个（确定的）$\left\{a_n\right\}$”的概率，记为$P(\left\{a_n\right\})$。

设$g[i]$为“前$i$个操作恰好为$\left\{a_n\right\}$的前$i$项”的概率，那么$P(\left\{a_n\right\})=g[n]$。

令$g[0]=1$。下面考虑$g[i]$的递推式。

$g[i]=\begin{cases}\frac{S_{i-1}+1}{i+1}g[i-1],\ a_i=1,\\ \frac{i-S_{i-1}}{i+1}g[i-1],\ a_i=0\end{cases}(i\ge 1)$

对上面的递推式用累乘法，发现一些事情：

• $g[n]$的分母一定是$2\times 3\times 4\times\cdots\times (n+1)=(n+1)!$

• 假设$a_i$之后下一个为$1$的项是$a_{i'}$，那么 $S_{i'-1}=S_{i-1}+1$。而$i$项的分子是 $S_{i-1}+1$，$i'$项的分子是 $S_{i'-1}+1=S_{i-1}+1+1$，知$i'$项的分子恰好比$i$项的分子多$1$。所以所有$a_i=1$项的分子是从$1$逐个递增到$S_n$的，所有$a_i=1$项的分子的乘积是$S_n!$

• 假设$a_i$之后下一个为$0$的项是$a_{i'}$，那么 $S_{i'-1}=S_{i-1}+(i'-1-i)$。而$i$项的分子是 $i-S_{i-1}$，$i'$项的分子是 $i'-S_{i'-1}=i'-(S_{i-1}+(i'-1-i))=i-S_{i-1}+1$，知$i'$项的分子恰好比$i$项的分子多$1$。一共有$n-S_n$项为$0$，它们的分子从$1$逐个递增到$n-S_n$，于是所有$a_i=0$项的分子的乘积是$(n-S_n)!$

那么就得到$P(\left\{a_n\right\})=\frac{S_n!(n-S_n)!}{(n+1)!}$。

上述几条结论不能推出来也没关系。“举例是理解的试金石”，我们不妨算一下$01$序列$010010$的概率。

$g[1]=\frac{1}{2}g[0]$，操作后$A$的元素数是$1$，$B$的元素数是$2$；

$g[2]=\frac{1}{3}g[1]$，操作后$A$的元素数是$2$，$B$的元素数是$2$；

$g[3]=\frac{2}{4}g[2]$，操作后$A$的元素数是$2$，$B$的元素数是$3$；

$g[4]=\frac{3}{5}g[3]$，操作后$A$的元素数是$2$，$B$的元素数是$4$；

$g[5]=\frac{2}{6}g[4]$，操作后$A$的元素数是$3$，$B$的元素数是$4$；

$g[6]=\frac{4}{7}g[5]$，操作后$A$的元素数是$3$，$B$的元素数是$5$.

把式子乘起来得到$g[6]=\frac{1\times 1\times 2\times 3\times 2\times 4}{2\times 3\times 4\times 5\times 6\times 7}=\frac{(1\times 2\times 3\times 4)\times (1\times 2)}{2\times 3\times 4\times 5\times 6\times 7}$

我们只是把$0$的分子和$1$的分子分开，就得到了结论。

或者，我们可以这么理解：概率的分子就是操作前这个集合中的元素个数。如果$A$集合要从$1$个元素变到$u+1$个元素（即序列中有$u$个$1$），必然经历了$1\rightarrow 2,2\rightarrow 3,\cdots,u\rightarrow u+1$的过程，这些过程中概率的分子之积自然是$u!$。$B$集合也是一样。

不管如何，我们现在得到了——操作序列是某个“含有$u$个$1$”的$01$串的概率是$\frac{u!(n-u)!}{(n+1)!}$（为方便描述，将上面推导过程中的$S_n$用$u$代替了）。从式子中我们发现，所有“含有$u$个$1$”的$01$串的概率是相等的。

当$u=t-1$时，操作结束后，$A$的元素数就是$t$。于是，“操作结束后，$A$的元素数就是$t$”的概率，就等于所有“含有$u$个$1$”的$01$串的概率之和。（这里用的是概率的加法原理，因为这些$01$串两两互斥（操作序列不可能同时为两个$01$串），且总事件全部由这些分事件所组成，因此可以这么计算。）

有多少“含有$u$个$1$”的$01$串呢？这是经典的子集问题，显然有$\mathrm{C}_n^u=\frac{n!}{u!(n-u)!}$个。

神奇的事情发生了——把$01$串数和每个$01$串的概率乘起来：

$\frac{n!}{u!(n-u)!}\times \frac{u!(n-u)!}{(n+1)!}=\frac{n!}{(n+1)!}=\frac{1}{n+1}$

于是就证完了……

（四）

$A$ 是非空有限集，且对于 $A$ 的所有非空子集 $S$，均有 $\left\{\varnothing \right\}\in S$ 或 $\left\{\varnothing \right\}\subseteq S$。求 $A$。