今天写了一遍KMP \text{KMP} KMP
首先是next \text{next} next next \text{next} next next \text{next} next next \text{next} next 如何更好的理解和掌握 KMP 算法? - 逍遥行的回答 - 知乎
下面对next \text{next} next
本文中next[i] \text{next[i]} next[i] s[0...i] \text{s[0...i]} s[0...i] 真 前缀又是真 后缀的最长子串的长度,如在字符串"aaaaa"中,next[4] = 4 \text{next[4]}=4 next[4] = 4
我们假设现在已经求出了next[0] ∼ next[i-1] \text{next[0]}\sim\text{next[i-1]} next[0] ∼ next[i-1] next[i] \text{next[i]} next[i] s[0] ∼ s[next[i-1]-1] \text{s[0]}\sim \text{s[next[i-1]-1]} s[0] ∼ s[next[i-1]-1] s[i-next[i-1]] ∼ s[i-1] \text{s[i-next[i-1]]}\sim \text{s[i-1]} s[i-next[i-1]] ∼ s[i-1] s[next[i-1]] \text{s[next[i-1]]} s[next[i-1]] s[i] \text{s[i]} s[i] next[i] \text{next[i]} next[i] next[i-1]+1 \text{next[i-1]+1} next[i-1]+1 s[next[i-1]] ≠ s[i] \text{s[next[i-1]]} \neq \text{s[i]} s[next[i-1]] = s[i] next[i] \text{next[i]} next[i] s[0] ∼ s[next[i]-2] \text{s[0]}\sim \text{s[next[i]-2]} s[0] ∼ s[next[i]-2] s[i-next[i]] ∼ s[i-1] \text{s[i-next[i]]}\sim \text{s[i-1]} s[i-next[i]] ∼ s[i-1] next[i-1] \text{next[i-1]} next[i-1]
我们经过探索知道,next[i] \text{next[i]} next[i] next[next[i]] \text{next[next[i]]} next[next[i]]
因此,我们的方法是,设一个变量t t t s[i]!=s[t] \text{s[i]!=s[t]} s[i]!=s[t] t > 0 t>0 t > 0 t t t next[ t − 1 ] \text{next[}t-1\text{]} next[ t − 1 ] next[i] \text{next[i]} next[i] t + 1 t+1 t + 1 0 0 0
求next[i] \text{next[i]} next[i]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void get_next (string &s) int l=s.size(); nxt[0 ]=0 ; for (int i=1 ;i<l;i++){ int t=nxt[i-1 ]; while (t && s[i]!=s[t]) t=nxt[t-1 ]; if (s[t]==s[i]) nxt[i]=t+1 ; else nxt[i]=0 ; } }
求next \text{next} next 已经完成,下面就是 比较简单的~~匹配过程了。
我们用i i i j j j j j j j = 0 j=0 j = 0 i = len ( a ) , j = len ( b ) i=\text{len}(a),j=\text{len}(b) i = len ( a ) , j = len ( b )
最后指出一点,洛谷的模板题实质上是MP \text{MP} MP KMP \text{KMP} KMP KMP \text{KMP} KMP next \text{next} next 这篇题解 ),但是两者在复杂度上没有差别,因此不再深究。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <iostream> #include <cstdio> #include <string> #define MAXN 1000005 using namespace std ;int nxt[MAXN]={0 };void get_next (string &s) int main (void ) string a,b; int i,j; int la,lb; cin >> a >> b; get_next(b); la=a.size(),lb=b.size(); i=j=0 ; while (i<la){ if (j==lb){ cout << i-lb+1 << endl ; j=nxt[j-1 ]; } if (a[i]==b[j]) i++,j++; else { if (j) j=nxt[j-1 ]; else i++; } } if (i==la && j==lb) cout << i-lb+1 << endl ; for (int i=0 ;i<lb;i++) cout << nxt[i] << ' ' ; cout << endl ; return 0 ; } void get_next (string &s) int l=s.size(); nxt[0 ]=0 ; for (int i=1 ;i<l;i++){ int t=nxt[i-1 ]; while (t && s[i]!=s[t]) t=nxt[t-1 ]; if (s[t]==s[i]) nxt[i]=t+1 ; else nxt[i]=0 ; } }
等一下,这篇文章还没完!如果KMP \text{KMP} KMP KMP \text{KMP} KMP 恋爱 循环有关的问题。
假设我们想要求一个字符串的最小循环节,如"abcabcabcabc"的最小循环节是"abc",“aaaaaaaa"的最小循环节是"a”,朴素的方法应该是进行O ( n 2 ) \text{O}(n^{2}) O ( n 2 ) KMP \text{KMP} KMP next \text{next} next O ( n ) \text{O}(n) O ( n )
来看一个定理。
定理 22.33 22.33 2 2 . 3 3
设一个字符串s [ 0... n − 1 ] \text{s}[0...n-1] s [ 0 . . . n − 1 ] n n n next [ n − 1 ] ≠ 0 \text{next}[n-1]\neq 0 next [ n − 1 ] = 0 ( n − next [ n − 1 ] ) ∣ n (n-\text{next}[n-1])\mid n ( n − next [ n − 1 ] ) ∣ n n ≡ 0 ( m o d n − next [ n − 1 ] ) n\equiv 0\pmod{n-\text{next}[n-1]} n ≡ 0 ( m o d n − next [ n − 1 ] ) 真 循环的(即循环次数大于1 1 1 n − next [ n − 1 ] n-\text{next}[n-1] n − next [ n − 1 ] n n − next [ n − 1 ] \frac{n}{n-\text{next}[n-1]} n − next [ n − 1 ] n s [ 0... n − 1 ] \text{s}[0...n-1] s [ 0 . . . n − 1 ] t t t next [ n − 1 ] = n − t \text{next}[n-1]=n-t next [ n − 1 ] = n − t t ∣ n t\mid n t ∣ n
证明:l = next[ n − 1 ] l=\text{next[}n-1\text{]} l = next[ n − 1 ] t = n − l t=n-l t = n − l n = k t ( k ∈ N ) n=kt(k\in \mathbb{N}) n = k t ( k ∈ N )
由于l ≠ 0 l\neq 0 l = 0 next \text{next} next l ≥ 0 l\ge 0 l ≥ 0 t < n t < n t < n
我们又有t ∣ n t\mid n t ∣ n n ≥ 2 t n\ge 2t n ≥ 2 t k ≥ 2 k\ge 2 k ≥ 2
由于l = n − t = k t − t = ( k − 1 ) t l=n-t=kt-t=(k-1)t l = n − t = k t − t = ( k − 1 ) t t ∣ l t\mid l t ∣ l
由于t t t l l l n n n s [ 0... n − 1 ] \text{s}[0...n-1] s [ 0 . . . n − 1 ] k k k t t t s [ 0... l − 1 ] \text{s}[0...l-1] s [ 0 . . . l − 1 ] s [ n − l . . . n − 1 ] \text{s}[n-l...n-1] s [ n − l . . . n − 1 ] k − 1 k-1 k − 1 t t t
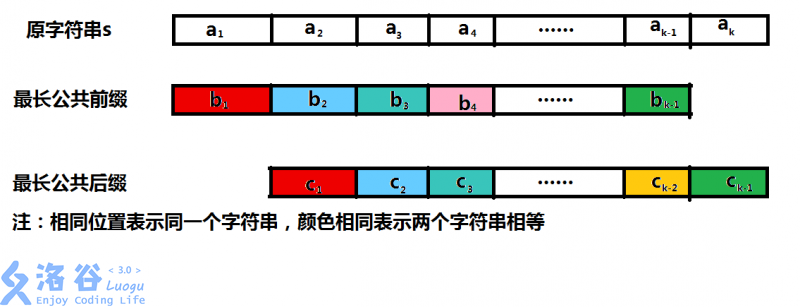
下面我们把s [ 0... n − 1 ] \text{s}[0...n-1] s [ 0 . . . n − 1 ] k k k a 1 , a 2 , ⋯ , a k a_{1},a_{2},\cdots,a_{k} a 1 , a 2 , ⋯ , a k s [ 0... l − 1 ] \text{s}[0...l-1] s [ 0 . . . l − 1 ] k − 1 k-1 k − 1 b 1 , b 2 , ⋯ , b k − 1 b_{1},b_{2},\cdots,b_{k-1} b 1 , b 2 , ⋯ , b k − 1 s [ n − l . . . n − 1 ] \text{s}[n-l...n-1] s [ n − l . . . n − 1 ] k − 1 k-1 k − 1 c 1 , c 2 , ⋯ , c k − 1 c_{1},c_{2},\cdots,c_{k-1} c 1 , c 2 , ⋯ , c k − 1
由next \text{next} next b 1 = c 1 , b 2 = c 2 , ⋯ , b k − 1 = c k − 1 b_{1}=c_{1},b_{2}=c_{2},\cdots,b_{k-1}=c_{k-1} b 1 = c 1 , b 2 = c 2 , ⋯ , b k − 1 = c k − 1
经过仔细比对下标范围~~(其实不那么仔细也可以)~~,我们又发现a 1 a_{1} a 1 b 1 b_{1} b 1 s \text{s} s
经过归纳得出a i a_{i} a i b i b_{i} b i i ∈ { i ∈ N ∣ 1 ≤ i ≤ k − 1 } i\in \{i\in \mathbb{N} \mid 1\le i \le k-1\} i ∈ { i ∈ N ∣ 1 ≤ i ≤ k − 1 } a i + 1 a_{i+1} a i + 1 c i c_{i} c i i ∈ { i ∈ N ∣ 1 ≤ i ≤ k − 1 } i\in \{i\in \mathbb{N} \mid 1\le i \le k-1\} i ∈ { i ∈ N ∣ 1 ≤ i ≤ k − 1 }
由b 1 = c 1 b_{1}=c_{1} b 1 = c 1 a 1 = a 2 a_{1}=a_{2} a 1 = a 2 b 2 = c 2 b_{2}=c_{2} b 2 = c 2 a 2 = a 3 a_{2}=a_{3} a 2 = a 3 b k − 1 = c k − 1 b_{k-1}=c_{k-1} b k − 1 = c k − 1 a k − 1 = a k a_{k-1}=a_{k} a k − 1 = a k a 1 = a 2 = ⋯ = a k a_{1}=a_{2}=\cdots=a_{k} a 1 = a 2 = ⋯ = a k s [ 0... t − 1 ] \text{s}[0...t-1] s [ 0 . . . t − 1 ] s \text{s} s
如何证明这是最小循环节呢?我们考察一个循环字符串,设它的最小循环节为"a",设"a"的长度为t ′ t' t ′ k k k n = k t ′ n=kt' n = k t ′ k − 1 k-1 k − 1 l = ( k − 1 ) t ′ l=(k-1)t' l = ( k − 1 ) t ′ t = n − l = t ′ t=n-l=t' t = n − l = t ′ t t t t ′ t' t ′ t t t
循环次数显然为n t \frac{n}{t} t n
整理可知,原命题和逆命题都已证毕。
下面附一张图以方便理解。
现在我们再来解决一个问题。如果一个字符串现在不是真循环字符串,我们现在可以在它的末尾补上若干个字符以使它成为真循环字符串,那么我们至少要补多少个字符呢?
这个问题其实也不难。要让它成为真循环字符串,只要让它满足恋爱 循环定理的条件即可,即让( n − next [ n − 1 ] ) ∣ n (n-\text{next}[n-1])\mid n ( n − next [ n − 1 ] ) ∣ n next [ n − 1 ] \text{next}[n-1] next [ n − 1 ] n n n l l l t t t
现在问题就转化成:求一个最小的正整数x x x t ∣ ( n + x ) t\mid (n+x) t ∣ ( n + x ) x = t − n % t x=t-n\%t x = t − n % t t − n % t t-n\%t t − n % t
总之,KMP \text{KMP} KMP next \text{next} next KMP \text{KMP} KMP
练习
KMP \text{KMP} KMP 求周期模板题 (数据范围比较小,但是可以作为练习)next \text{next} next next \text{next} next 记得开long long \text{long long} long long )
上述两个next \text{next} next next \text{next} next next \text{next} next